True umbral and antumbral surfaces of the lunar shadow (C) 2013-2019 John Irwin

True Umbral and Antumbral Surfaces of the Lunar Shadow

The images shown below were created to illustrate the three-dimensional structure of the Moon's shadow and its relationship with the smooth-limb shadow cone. The true shape of the shadow is due entirely to the rugged nature of the lunar surface and is especially interesting in the region of the smooth cone apex, as we shall see for three particular solar eclipses, two of which were visited by airborne observers.

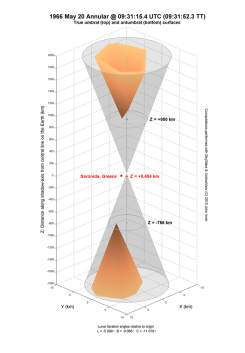
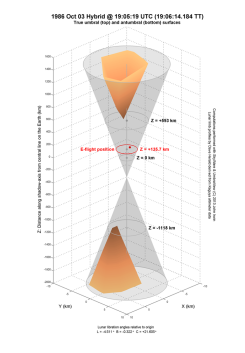
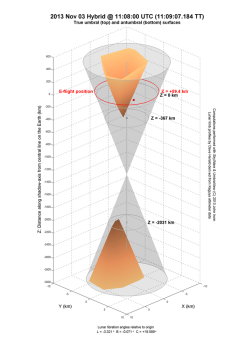
The time in each case is close to maximum eclipse experienced by the observers on the ground at the annular eclipse of 1966 and by E-flight missions to the hybrid eclipses in 1986 and 2013 which attempted to view totality from 44000 feet above the Earth's surface. Note that all three eclipses have a magnitude close to unity for ground-based observers.

The X-, Y-, and Z-axes in these images are parallel to the corresponding coordinate axes of the Fundamental Plane frame but the origin has been translated to the point on the Earth's surface where the shadow-axis intersects it – in other words the point on the topocentric central line at this time. The X-axis points due east; the Y-axis points due north; and the Z-axis points towards the centres of the Sun and Moon. The view in each case is from the north-east at an elevation of 25°. Note that the Z-axis is highly compressed compared to the other two axes, the effect of which is to open up the shadow cones considerably. So while the X- and Y-axes only span 20 km each, the Z-axis covers 3600 km or more. In reality the smooth-limb cone angle is only about 0.25° and the cone itself is very needle-like.

ASE1966	HSE1986	HSE2013

	Follow the image links to see full-sized versions of each plot.

The umbral/antumbral surfaces are shown by the orange-shaded objects at the top and bottom of the image. Each object is composed of about 32000 facets, which is more than enough resolution to faithfully reproduce the shape of the true surfaces at this scale. Of course, the umbral surface extends all the way back to the Moon while the antumbral surface continues into deep space (if the Earth weren't in the way) but they have been truncated here for the purpose of illustration. The truncation of the umbral surface also helps us to see the actual polygonal shape of the true shadow outline.

The smooth-limb cone is rendered in a neutral transparent colour. Along this cone, perpendicular cross-sections have been drawn corresponding to the Z-coordinates of the tips of the umbral and antumbral surfaces, as well as one for the zero-Z level (if there's room to show it). A section through the observer position is also shown in red, the red point locating the actual position, either on the ground or in the air.

Remember what the true umbral/anutumbral surfaces represent – they are a geometric boundary separating locations which can see a total or annular eclipse from those that can't. This is exactly how you would treat the smooth-limb cone if no limb-corrections were considered. So we can see that the introduction of a lunar limb profile greatly alters the cone appearance and in the process separates the umbral and antumbral parts by a not insignificant distance. As you may deduce, this separation is 1702 km for ASE1966, 1711 km for HSE1986, and 1664 km for HSE2013.

You will notice that the observers of the 1966 eclipse are located outside the smooth-limb shadow cone. This contradicts predictions made at the time which had placed them inside the antumbral path on the ground. The apparent discrepancy is simply due to my using a non-reduced lunar radius for the calculation of the smooth-limb cone. It is common practise to use a slightly smaller radius to get a better estimation of the true contact times of total eclipses, although it is arguable whether this practise should be followed for annulars (in which case an enlarged radius would seem appropriate). Using a reduced radius would cause the smooth cone apex to fall nearer the Moon (upwards in the image), pulling up the antumbral cone sufficiently to enclose the observer position. In any case this is a moot point as the observers saw neither a total nor annular eclipse that day. Their position relative to the true lunar shadow clearly shows why only a brief broken eclipse was observed. However, out of these three eclipses, the observers of the 1966 eclipse were positioned most symmetrically between the true umbral and antumbral shadows and would have witnessed a spectacular amount of beading during this brief period.

We can also see for the E-flight eclipses that while both flights crossed the smooth-limb cone, neither penetrated the true umbral surface. This is consistent with the observations from each eclipse which reported no complete obscuration of the Sun.

The 1986 flight passed by the shadow-axis at a distance of about 1.1 km but it was some 457 km "below" the umbral surface so had no chance of encountering totality. I think you would have needed to get into low orbit to see that one. Notice that the umbral surface in 1986 is far the Earth's surface at this time. This means that totality was not even possible for ground-based (or should I say ship-based) observers and this in fact was true for the whole of the topocentric central line.

The 2013 flight was more favourable. The umbral surface reached all the way down to and through the Earth's surface so it was just a matter of getting above the clouds. Unfortunately this flight had computer/navigation problems and just missed totality. It came within about 4.1 km of the shadow-axis and about 2 km from the umbral surface.

The main thing to take from these visualisations is the presence of the gap between the true umbral and antumbral shadows. This is a natural feature of the Moon's shadow and is not peculiar to near-unity-magnitude eclipses (or any eclipse, for that matter). However, for these sorts of eclipses the gap has a close relationship with the Earth's surface and greatly influences whether totality or annularity, if either, will occur for any particular location on or near the Earth's surface.

This close relationship also affects the shape of the central path (on the surface of the Earth for example) with the consequence that the path limits may not exist for all points along the central line. This leads to a new central line property which we may call nakedness. This is the case for HSE2013 where the central path does not span the full length of the central line (it is naked for a small section leading from the sunrise start of the line and for a small section trailing into the sunset end). HSE1986 is an extreme example in that the central path on the Earth's surface does not exist at all – a central line, yes, but no definable outline, no limit lines, and therefore no path. A totally naked central line, one may say.

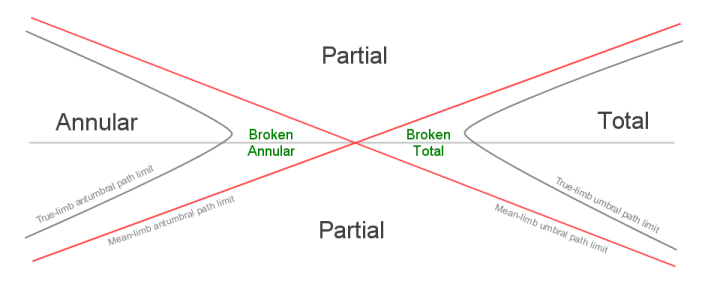
With this in mind, we can now visualise in a schematic way the layout of the central path around the transition point of an hybrid eclipse (see image below) and to suggest a more robust definition of a broken eclipse.

The image shows the central path around the A-T transition region for both the smooth (mean) limb and the true limb. In each case, the path limits are the result of the movement of the 3D shadow cones across the 2D surface of the Earth (or level of interest above the Earth). The path for the smooth limb will be familiar, consisting of the transition point where the shadow cone apex moves through the Earth's surface. But for the true shadow "cones" there is the gap to consider and this produces a corresponding gap in the central path.

Note how the ends of the true path are displaced from the central line to reflect the fact that the ends do not necessary lie on the shadow axis (and seem to occur on the same side of the axis but that may not always be the case). Note also that the transition point falls roughly mid-way between the ends of the true path. This would correspond to the path for a mean lunar radius. Otherwise if a reduced radius is used, the transition point would be closer to the end of the total path.

The true path limits have been drawn as smooth lines which, by-and-large, they would be except for small discontinuous changes of slope, or a more substantial change at the ends of the path. Not shown here, but there's also the possibility that the true path limit line will cross the smooth path limit line. So it's quite possible for a nominally-determined partial eclipse to be observed as an annular or total. It could also correspond to the situation where the duration increases with limb corrections and this would be more likely for a smooth path determined from a reduced lunar radius.

Definition: The region between the true and smooth path limits shows where a broken eclipse will be seen and can be described either as broken annular or as broken total depending on which side of the transition point an observer is situated.

As yet there is no mathematical means to determine the actual path limits for the true shadow. Any such determination would need to be done numerically, similar to how the 3D shadow surfaces have been generated. This would not be an easy calculation as it would involve estimating the intersection of a polygonal surface (albeit hi-res) with the Earth's ellipsoid. But not impossible and the near future may show us the way forward.

First published 8 December 2013. This update 23 May 2019